La théorie de la relativité restreinte nous enseigne que matières ou ondes ne peuvent atteindre la vitesse de la lumière. C'est une question d'énergie disponible, à mesure que l'objet approche de cette vitesse, sa masse relative augmente exponentiellement. Si bien que lorsque la vitesse tend vers « c » l'énergie nécessaire à son déplacement tend vers l'infini.
Heureusement, Star Trek est une série d'une grande logique et ne cherche pas à violer ouvertement (du moins pas souvent, sinon, les responsables se feraient vertement fustiger par nous les Admirateurs) les lois de la physique admises par tous. Au contraire, elle explique et tente de justifier, du moins partiellement la plupart des technologies que l'on voit à l'écran.
Les facteurs de distorsions dont il est souvent fait mention dans notre univers préféré font cependant figure d'exceptions. Ceci tient surtout au fait qu'ils ont été conçus en ingénierie inversée, ce qui n'enlève rien à l'imagination dont font preuve les scénaristes et producteurs. Mais nous rend la tâche pénible lorsque nous voulons calculer ces paramètres.
Échelle de Cochrane
L'échelle originale (TOS) ou échelle de Cochrane avait une base mathématique simple, elle était constituée d'une série de cubes successifs, ne tenant pas compte de l'énergie employée pour propulser le vaisseau. Des facteurs de 10 et plus étaient alors tout à fait concevables.
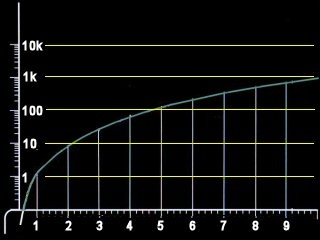
Vous remarquerez que ce graphique est constitué d'une échelle logarithmique sur l'axe des ordonnées (Y) composées de multiples de (c) et d'une échelle linéaire sur l'axe des abscisses (X) qui indiquent les facteurs de distorsions. Le maximum atteignable devait être distorsion 21, mais n'a jamais été vu à l'écran.
Une formule simple s'applique à ce graphique, V = f ^ 3 x c ou en toutes lettres « la vitesse est égale au facteur de distorsion élevé au cube multiplié par c »
Exemple, Vitesse = 2 ^ 3 x 299792 soit 2 398 339,664 km/s.
L'opération inverse f = 3√v/c ou en toutes lettres « le facteur de distorsion est égal à la racine cubique de la vitesse divisée par c » est également facile à réaliser.
Exemple, facteur de distorsion = 3√ 2 398 339,664/299792 soit facteur 2.
N'oubliez pas que si vous calculez un facteur ou une vitesse, vos unités doivent être équivalentes.
Bien qu'il n'y ait pas de documentation officielle sur ce point, je suis convaincu que l'exposant 3 utilisé n'est pas dût au hasard, il correspond au poids atomique du Lithium (un métal alcalin solide) entrant dans la composition des cristaux de Dilithium utilisé pour réguler la réaction matière/antimatière dans les moteurs de distorsion.
Échelle TNG
Gene Roddenberry tenait absolument à ce que la distorsion 10 représente un seuil infini, impossible à atteindre. C'est pourquoi Michael Okuda dessina une nouvelle échelle de 1 à 9 basée sur le facteur élevé à la puissance 10/3 (3.3333). Pour les facteurs plus grands que 9 jusqu'à 9.99999, il a simplement tracé (sans avoir recours aux mathématiques) une courbe ascendante qui atteint une valeur asymptotique à 10. Ensuite, il a intégré une courbe reflétant la puissance requise pour passer d'un facteur à l'autre, ce qui justifie la valeur infinie.
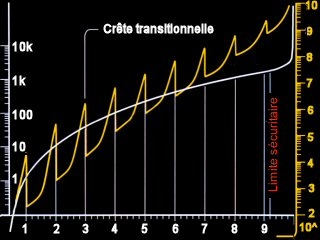
D'ailleurs, il est facile de noter avec ce graphique qu'il est plus économique énergétiquement parlant pour un vaisseau de naviguer à distorsion 6 qu'à 5,8 par exemple.
Vous remarquerez qu'il y a une grande différence de vitesse entre les facteurs de l'échelle de Cochrane et celle-ci.
Là où ça coince!
De 1 à 9, les facteurs ont été arrondis.
Exemple :
2 ^ 10/3 = 10,0793684 arrondi à 10
5 ^ 10/3 = 213,7469933 arrondit à 214
Il n'y a que le facteur 8 qui arrive pile, sans arrondis
Pour les facteurs plus grands que 9, on doit augmenter l'exposant graduellement de manière à ce que le résultat obtenu soit conforme au tableau. Donc dans ce cas pas de méthode simple pour le calcul.
Ajoutez à ceci le mode de trans-distorsion, qui serait en fait une autre manipulation de l'échelle TNG pour les facteurs plus grand que 9.9.
Dans ce mode facteur 10 est 9.9 tng, 11 est 9.99 tng, 12 est 9.999 tng. Et ainsi de suite.
Des heures de plaisir mathématique en perspective!
L'ensemble des calculs de distorsion sont disponibles sur notre
Calculateur...

 WebTopaze
WebTopaze
 Vous remarquerez que ce graphique est constitué d'une échelle logarithmique sur l'axe des ordonnées (Y) composées de multiples de (c) et d'une échelle linéaire sur l'axe des abscisses (X) qui indiquent les facteurs de distorsions. Le maximum atteignable devait être distorsion 21, mais n'a jamais été vu à l'écran.
Vous remarquerez que ce graphique est constitué d'une échelle logarithmique sur l'axe des ordonnées (Y) composées de multiples de (c) et d'une échelle linéaire sur l'axe des abscisses (X) qui indiquent les facteurs de distorsions. Le maximum atteignable devait être distorsion 21, mais n'a jamais été vu à l'écran.


 Bok, un commandant Ferengi, offre à Picard l'épave du Stargazer supposé perdu. Ce cadeau se révèle vite n'être qu'un piège destiné à venger une ancienne bataille perdue par les Ferengis lorsque Picard était capitaine de l'USS Stargazer.
Bok, un commandant Ferengi, offre à Picard l'épave du Stargazer supposé perdu. Ce cadeau se révèle vite n'être qu'un piège destiné à venger une ancienne bataille perdue par les Ferengis lorsque Picard était capitaine de l'USS Stargazer.
Sur ce coup, tu nous gâte, il est détaillé et bien expliqué.